Wiskunde is geen rekenen! - ΩJr. Wiskunde en Bijles
Deze informatie leeft op een webpagina op hetvolgende webadres: 'https://omegajunior.globat.com/wiskunde/'.
Hoensbroek,
A.E.Veltstra, 28-12-2001
Hoewel rekenkunde noodzakelijk lijkt om wiskunde te kunnen beoefenen, heeft wiskunde heel weinig met rekenen te maken. Er zijn overeenkomsten, jazeker, en met enig geduld kan aangetoond worden dat wiskunde een moeilijker, verderdragend vak is, gebaseerd op rekenkunde.
Maar daar houden de overeenkomsten op.
Dit is geen essay. Dit is meer een pamflet. De gedachten die hier worden weergegeven, zijn niet doorgekauwd.
Niettemin vind ik ze belangrijk genoeg om te publiceren.
Ik ben informatiesysteemontwikkelaar. Ik help organisaties bij het vormgeven van hun informatiesystemen.
Deze worden meestal geautomatiseerd, en tot een serie computerprogramma's verwerkt. Het omzetten van informatiesystemen in een computerprogramma is een formaliserend proces.
Zaken die door mensen gemakkelijk begrepen worden, zijn voor een computer alleen begrijpelijk door strikte algoritmen te volgen. Het interessante nu van automatisering is, dat je die algoritmen zelf moet schrijven.
Het schrijven van algoritmen is iets, dat je al geleerd krijgt op de middelbare school, tijdens wiskunde. Er wordt alleen een ander woord voor gebruikt: "formule".
Heerlijke apparaten, die grafische rekenmachines.
Je krijgt een formule van je leraar, leert de formule uit je hoofd of programmeert hem in de rekenmachine, vult de juiste cijfers op de juiste plaats in, en voilà, de uitkomst. Tabellen, grafieken, zelfs bewerkingen om op de formule los te laten, alles staat ter beschikking.
Je hoeft niet te kunnen rekenen om tot een uitkomst te komen. Er is geen enkel vak op de middelbare school waarin je hoeft te kunnen rekenen.
Dat antwoord is meestal een getal, al dan niet met een maateenheid. Als het antwoord juist is, neemt de leraar aan dat de gevolgde methode ook juist is, en dat de leerling de stof begrepen heeft.
Een voorbeeld:
Gegeven is de driehoek abc, met lengte ac = 5 meter, hoek c = 90° en hoek a = 45°. Gevraagd: de lengte van zijde cb.
Nu krijgen de leerlingen op mavo 4 het ezelsbruggetje "soscastoa" aangeleerd. Uitgewerkt staat dat voor "sinus = overstaande / schuine; cosinus = aanliggende / schuine; tangens = overstaande / aanliggende".
Tevens kun je met enige oefening leren welke van de zijden van een driehoek de overstaande, de schuine of de aanliggende zijde is.
In de voorbeeldopgave moet de tangensformule gebruikt worden: "tangens = overstaande / aanliggende", oftewel "tan(45°) = cb / 5m". Omgewerkt wordt dat "cb = 5m * tan(45°)".
Dit lijkt rechttoe-rechtaan.
Totdat je merkt, dat veel leerlingen die laatste omwerking fout doen, en opeens gaan delen in plaats van vermenigvuldigen.
Delen?
Jazeker.
Ze snappen niet waarom er vermenigvuldigd moet worden, en gaan gokken.
De omwerking "(3 = 6 / 2) dus (6 = 3 * 2)" wordt wel aangeleerd, maar menig leerling leert dit nooit toepassen op goniometrie. Er is 50% kans op een goede methode (òf delen, òf vermenigvuldigen), zodat de leerlingen een groot deel van de antwoorden goed hebben.
Daar er beoordeeld wordt op de antwoorden, en niet op de methode, laten vele leerlingen het hierbij.
Wat maakt het hen uit, dat er enkele fouten tussen staan?
De leerling heeft niet in de gaten dat hij niet weet wat de juiste methode is, want een groot deel van de antwoorden is goed. Nog erger is, dat de leraar niet in de gaten krijgt dat de leerling op "gevoel" afgaat, met andere woorden gokt tussen delen en vermenigvuldigen, en hierbij soms goed, en soms fout gokt.
De leraar ziet niet dat de leerling niet weet wat de juiste methode is.
En daarmee komen we bij het hart van het probleem:
"5 / 45 tan = 5".
Dat komt, uiteraard, omdat de tangens van 45° gelijk is aan 1.
Maar de verhouding tussen hoek en tangens, sinus en cosinus wordt de leerlingen niet bijgebracht. Alleen de formule wordt hen aangeleerd.
Het juiste antwoord is "cb = 5m * tan(30°) = 2,89m".
Als de leerling fout gokt, en gaat delen, komt het volgende foutieve antwoord: "cb = 5m / tan(30°) = 8,66m".
Stel je nu voor dat de leerling voldoende tijd heeft op het proefwerk, en daadwerkelijk nadenkt over de realiteit van het gegeven antwoord, dan komt hij erachter dat een kleinere hoek ook een kleinere lengte cb inhoudt, en dat het gegeven antwoord fout moet zijn. Maar welke leerlingen hebben voldoende tijd? Dat zijn diegenen die toch al weten waar ze mee bezig zijn, en de opgaven waarschijnlijk al correct hebben beantwoord.
Juist de leerlingen die de antwoorden niet goed hebben, zijn degenen die daar niet achterkomen.
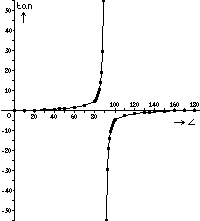
Als de hoek groter wordt, dan wordt de tangens van de hoek ook groter, tot aan 90°. Bij 90° is de tangens oneindig groot, en na 90° komt de grafiek puntgespiegeld terug. Bij 180° is de tangens weer 0, en begint de grafiek weer van voor af aan.
Als de leerling de grafiek ongeveer zou kennen (het zou al voldoende zijn als de leerling wist dat het een positieve hyperbool was, met het spiegelpunt op coördinaat (90,0)), zou hij kunnen inschatten wat het gevolg zou zijn van delen en vermenigvuldigen, en aan de hand daarvan de juiste berekening kunnen kiezen.
Hij krijgt geen verklaring aangeleerd, hij krijgt een formule, een truukje.
En met dat truukje moet gewerkt worden.
Omdat de leerling geen inzicht heeft in de werking van goniometrie, heeft hij niet geleerd hoe hij zijn eigen werk kan nakijken, heeft hij niet in de gaten dat hij op de foute methode gegokt heeft, en kan zijn eigen fout niet verbeteren. De leerling heeft geen andere keus dan de waarden in te voeren in de rekenmachine, en erop te vertrouwen dat de machine het juiste antwoord ophoest.
De leerling leert te gokken, in plaats van op te lossen. Hij leert te vertrouwen op zijn gave het juiste truukje uit te kiezen, in plaats van zijn gave te beredeneren welke oplossingsmethode correct is.
Hij kent wel de drie formules, zoals "tangens = overstaande / aanliggende".
De formules worden echter niet in verband gebracht met de rest van de wiskunde, met cirkels, met vergrotingen en spiegelingen, met hogeremachts- en gedeelde formules. Pas als de hele wereld om de goniometrie samenhangend verklaard is, is de leerling in staat een mentaal beeld te schetsen, en te begrijpen waarom hij moet vermenigvuldigen in plaats van delen (of andersom).
Dat geldt niet alleen voor goniometrie, maar voor alle onderdelen van wiskunde.
Het is gedeeltelijk abstract en gedeeltelijk realistisch, oftewel gedeeltelijk uitgedrukt in letters, en gedeeltelijk ingevuld met cijfers.
2. Laat de leerling tijdens het oplossen alleen abstract werken, totdat de complete oplossing uitgewerkt is.
3. Laat de leerling voor elke opgave een formule creëren, waarin geen enkel cijfer is opgenomen.
4.Laat deze formule het antwoord zijn op de vraag.
Ik heb menig leerling zomaar wat zien uitproberen, en als er een antwoord verscheen dat ongeveer zou kunnen kloppen, werd het als oplossing aangegeven.
Leerlingen doen dat voornamelijk als ze niet zeker van de oplossingsmethode zijn, en ook als de methode zo moeilijk is dat de oplossing niet makkelijk voorstelbaar is.
Spelen met getallen is een leuke bezigheid en ontwikkelt gevoel voor berekeningen, maar is niet de juiste methode om een opgave op te lossen.
Ten tweede is het aan de door de leerling gevonden formule direct zichtbaar of de methode begrepen is, in tegenstelling tot een antwoord in cijfers. Dit is vooral van belang als de cijfers zonder meer in de rekenmachine ingevoerd kunnen worden.
Ten derde is het mogelijk om berekeningensoplossingen uit je hoofd te leren, zodat je niet hoeft te rekenen. We doen niets anders, wanneer we tafeltjes leren. Als de oplossing van de opgave een formule is, zijn er geen standaard antwoorden uit je hoofd te leren. Dan wordt je gedwongen de juiste methode te gebruiken, en elke stap naar de oplossing correct uit te voeren.
Ten vierde zorgt deze methode ervoor dat de leerling gaat herkennen hoe de verschillende oplossingsmethoden met elkaar samenhangen, ontdekt dat de opgaven in dezelfde paragraaf steeds met dezelfde methode opgelost kunnen worden, in plaats van te menen dat elke opgave een uitzondering is en op een andere manier opgelost moet worden.
Ten vijfde maakt dit enkele onderdelen van de wiskunde makkelijker, zoals het opstellen van formules voor lineaire en hogeremachtsfuncties, evenals later het schrijven van computeralgoritmes.
Ten zesde, en waarschijnlijk ten belangrijkste, leert de leerling om algoritmen te creëren voor wiskundige bewerkingen buiten de wiskunde, in de andere exacte vakken.
Maar wiskundeleerlingen leren toch al niet rekenen. Zij moeten al kunnen rekenen voordat ze wiskunde kunnen leren.
Je leert aan, hoe je formules op een rekenmachine uitwerkt.
Ik heb leerlingen die na drie jaar middelbare school de simpelste berekening met de rekenmachine moeten uitvoeren, omdat "dat sneller gaat", of ze "het anders niet weten".
Dat is triest.
Daarom naast het bovenstaande voorstel een tweede:
Leer ze uitkomsten te schatten van wortels en machten, leer ze waar ze mogen gokken en waar niet.
Leer leerlingen hoe zij hun eigen oplossingen kunnen controleren.
Scheid wiskunde van rekenen, zodat leerlingen het verschil herkennen tussen het opstellen van algoritmen om van een opgave naar een oplossing te komen, en het bewerken van getallen.
En als laatste een oproep aan wiskundeleraren en het Ministerie van Onderwijs:
De rekenmachine is heel goed in staat alle berekeningen voor je uit te voeren en genereert rekenkundig gemakzucht.
Wiskunde moet zich contentreren op het creëren van algoritmen, naar de vraag "hoe los ik dit op?" in plaats van naar de vraag "wat is de oplossing?".
Deze worden meestal geautomatiseerd, en tot een serie computerprogramma's verwerkt. Het omzetten van informatiesystemen in een computerprogramma is een formaliserend proces.
Zaken die door mensen gemakkelijk begrepen worden, zijn voor een computer alleen begrijpelijk door strikte algoritmen te volgen. Het interessante nu van automatisering is, dat je die algoritmen zelf moet schrijven.
Het schrijven van algoritmen is iets, dat je al geleerd krijgt op de middelbare school, tijdens wiskunde. Er wordt alleen een ander woord voor gebruikt: "formule".
Je hoeft niet te kunnen rekenen om formules te bouwen.
Het bouwen van formules volgt richtlijnen die in de loop van de afgelopen 3000 jaar zijn ontwikkeld. Je moet wel kunnen rekenen om formules te controleren, en wie niet kan rekenen, kan een (grafische) rekenmachine gebruiken.Heerlijke apparaten, die grafische rekenmachines.
Je krijgt een formule van je leraar, leert de formule uit je hoofd of programmeert hem in de rekenmachine, vult de juiste cijfers op de juiste plaats in, en voilà, de uitkomst. Tabellen, grafieken, zelfs bewerkingen om op de formule los te laten, alles staat ter beschikking.
Je hoeft niet te kunnen rekenen om tot een uitkomst te komen. Er is geen enkel vak op de middelbare school waarin je hoeft te kunnen rekenen.
Om te rekenen, heb je de rekenmachine en zijn handleiding.
Laten we eens gaan kijken naar de manier waarop wiskundeproefwerken worden afgenomen. De bedoeling van het proefwerk is te testen of de leerling de stof begrepen heeft.Maar hoe gebeurt dat bij wiskunde?
De leraar stelt enkele opgaven ter beschikking, maar heeft bij het nakijken geen tijd om te beoordelen of de leerling de juiste methode heeft gebruikt. Dit wordt afgeleid aan de juistheid van het antwoord dat op de opgaven is gegeven.Dat antwoord is meestal een getal, al dan niet met een maateenheid. Als het antwoord juist is, neemt de leraar aan dat de gevolgde methode ook juist is, en dat de leerling de stof begrepen heeft.
Niet alleen proefwerken gebruiken deze methode, het huiswerk zelf ook.
Om het huiswerk na te kijken, zijn er twee verschillende lerarenboeken: 1 het oplossingenboek, met daarin alleen per opgave de oplossing, en 2 het uitwerkingenboek, met daarin per opgave de complete gebruikte methode, toegepast op de getallen die in de opgave worden gebruikt.Er gaat iets fundamenteels mis met deze vorm van beoordeling.
Dit wordt duidelijk aan de hand van het wiskundeonderdeel Goniometrie. Op 4 mavo wordt goniometrie teruggebracht tot het uitrekenen van lengten van zijden van driehoeken.Een voorbeeld:
Gegeven is de driehoek abc, met lengte ac = 5 meter, hoek c = 90° en hoek a = 45°. Gevraagd: de lengte van zijde cb.
Nu krijgen de leerlingen op mavo 4 het ezelsbruggetje "soscastoa" aangeleerd. Uitgewerkt staat dat voor "sinus = overstaande / schuine; cosinus = aanliggende / schuine; tangens = overstaande / aanliggende".
Tevens kun je met enige oefening leren welke van de zijden van een driehoek de overstaande, de schuine of de aanliggende zijde is.
In de voorbeeldopgave moet de tangensformule gebruikt worden: "tangens = overstaande / aanliggende", oftewel "tan(45°) = cb / 5m". Omgewerkt wordt dat "cb = 5m * tan(45°)".
Dit lijkt rechttoe-rechtaan.
Totdat je merkt, dat veel leerlingen die laatste omwerking fout doen, en opeens gaan delen in plaats van vermenigvuldigen.
Delen?
Jazeker.
Ze snappen niet waarom er vermenigvuldigd moet worden, en gaan gokken.
De omwerking "(3 = 6 / 2) dus (6 = 3 * 2)" wordt wel aangeleerd, maar menig leerling leert dit nooit toepassen op goniometrie. Er is 50% kans op een goede methode (òf delen, òf vermenigvuldigen), zodat de leerlingen een groot deel van de antwoorden goed hebben.
Daar er beoordeeld wordt op de antwoorden, en niet op de methode, laten vele leerlingen het hierbij.
Wat maakt het hen uit, dat er enkele fouten tussen staan?
De leerling heeft niet in de gaten dat hij niet weet wat de juiste methode is, want een groot deel van de antwoorden is goed. Nog erger is, dat de leraar niet in de gaten krijgt dat de leerling op "gevoel" afgaat, met andere woorden gokt tussen delen en vermenigvuldigen, en hierbij soms goed, en soms fout gokt.
De leraar ziet niet dat de leerling niet weet wat de juiste methode is.
En daarmee komen we bij het hart van het probleem:
Hoe berekent de leerling "cb = 5m * tan(45°)"?
Simpelweg door de grafische rekenmachine te pakken en in te typen: "5 * 45 tan =". De rekenmachine geeft het antwoord: "5".Het vervelende is, dat je ook kunt delen,
en dan ook het antwoord "5" krijgt:"5 / 45 tan = 5".
Dat komt, uiteraard, omdat de tangens van 45° gelijk is aan 1.
Maar de verhouding tussen hoek en tangens, sinus en cosinus wordt de leerlingen niet bijgebracht. Alleen de formule wordt hen aangeleerd.
Dit levert de volgende situatie op:
Gegeven is de driehoek abc, met lengte ac = 5 meter, hoek c = 90° en hoek a = 30°. Gevraagd: de lengte van zijde cb.Het juiste antwoord is "cb = 5m * tan(30°) = 2,89m".
Als de leerling fout gokt, en gaat delen, komt het volgende foutieve antwoord: "cb = 5m / tan(30°) = 8,66m".
Stel je nu voor dat de leerling voldoende tijd heeft op het proefwerk, en daadwerkelijk nadenkt over de realiteit van het gegeven antwoord, dan komt hij erachter dat een kleinere hoek ook een kleinere lengte cb inhoudt, en dat het gegeven antwoord fout moet zijn. Maar welke leerlingen hebben voldoende tijd? Dat zijn diegenen die toch al weten waar ze mee bezig zijn, en de opgaven waarschijnlijk al correct hebben beantwoord.
Juist de leerlingen die de antwoorden niet goed hebben, zijn degenen die daar niet achterkomen.
Een oplossing voor deze situatie
De leerling zou ook de grafiek van de verhouding tussen tangens en hoek kunnen kennen, maar dat is in de wiskundeles niet aan bod gekomen.Deze grafiek ziet er zo uit:

Als de hoek groter wordt, dan wordt de tangens van de hoek ook groter, tot aan 90°. Bij 90° is de tangens oneindig groot, en na 90° komt de grafiek puntgespiegeld terug. Bij 180° is de tangens weer 0, en begint de grafiek weer van voor af aan.
Als de leerling de grafiek ongeveer zou kennen (het zou al voldoende zijn als de leerling wist dat het een positieve hyperbool was, met het spiegelpunt op coördinaat (90,0)), zou hij kunnen inschatten wat het gevolg zou zijn van delen en vermenigvuldigen, en aan de hand daarvan de juiste berekening kunnen kiezen.
Maar niets van dat alles.
De leerling krijgt geen inzicht in de werking, noch de resultaten van goniometrie.Hij krijgt geen verklaring aangeleerd, hij krijgt een formule, een truukje.
En met dat truukje moet gewerkt worden.
Elke aap kan truukjes leren.
Maar de drie formules voor sinus, cosinus en tangens moeten regelmatig omgewerkt worden, wat de helft van de tijd foutgaat omdat er geen samenhangend stelsel is aangeleerd.Omdat de leerling geen inzicht heeft in de werking van goniometrie, heeft hij niet geleerd hoe hij zijn eigen werk kan nakijken, heeft hij niet in de gaten dat hij op de foute methode gegokt heeft, en kan zijn eigen fout niet verbeteren. De leerling heeft geen andere keus dan de waarden in te voeren in de rekenmachine, en erop te vertrouwen dat de machine het juiste antwoord ophoest.
De leerling leert te gokken, in plaats van op te lossen. Hij leert te vertrouwen op zijn gave het juiste truukje uit te kiezen, in plaats van zijn gave te beredeneren welke oplossingsmethode correct is.
Dat is niet zo vreemd als het lijkt.
De leerling krijgt niet aangeleerd waar dat nu vandaan komt, sinus, cosinus en tangens.Hij kent wel de drie formules, zoals "tangens = overstaande / aanliggende".
De formules worden echter niet in verband gebracht met de rest van de wiskunde, met cirkels, met vergrotingen en spiegelingen, met hogeremachts- en gedeelde formules. Pas als de hele wereld om de goniometrie samenhangend verklaard is, is de leerling in staat een mentaal beeld te schetsen, en te begrijpen waarom hij moet vermenigvuldigen in plaats van delen (of andersom).
Helaas is daar geen tijd voor.
Goniometrie is een oude tak van wiskunde, en de middelbare school heeft geen tijd om er breed op in te gaan, laat staan diep.Dat geldt niet alleen voor goniometrie, maar voor alle onderdelen van wiskunde.
Wiskunde op de middelbare school moet in een zo kort mogelijke tijd 3000 jaar ontwikkeling in een leerling stampen.
Ik vermoed dat het probleem van "gokken naar een oplossing" voortkomt uit de halfslachtigheid van de wiskunde:Het is gedeeltelijk abstract en gedeeltelijk realistisch, oftewel gedeeltelijk uitgedrukt in letters, en gedeeltelijk ingevuld met cijfers.
Ik zou het volgende willen uitproberen.
1. Laat een leerling geen enkel getal invullen.2. Laat de leerling tijdens het oplossen alleen abstract werken, totdat de complete oplossing uitgewerkt is.
3. Laat de leerling voor elke opgave een formule creëren, waarin geen enkel cijfer is opgenomen.
4.Laat deze formule het antwoord zijn op de vraag.
Er zijn een aantal redenen voor dit voorstel:
Ten eerste gaat een leerling niet meer zomaar wat uitproberen met cijfers en berekeningen.Ik heb menig leerling zomaar wat zien uitproberen, en als er een antwoord verscheen dat ongeveer zou kunnen kloppen, werd het als oplossing aangegeven.
Leerlingen doen dat voornamelijk als ze niet zeker van de oplossingsmethode zijn, en ook als de methode zo moeilijk is dat de oplossing niet makkelijk voorstelbaar is.
Spelen met getallen is een leuke bezigheid en ontwikkelt gevoel voor berekeningen, maar is niet de juiste methode om een opgave op te lossen.
Ten tweede is het aan de door de leerling gevonden formule direct zichtbaar of de methode begrepen is, in tegenstelling tot een antwoord in cijfers. Dit is vooral van belang als de cijfers zonder meer in de rekenmachine ingevoerd kunnen worden.
Ten derde is het mogelijk om berekeningensoplossingen uit je hoofd te leren, zodat je niet hoeft te rekenen. We doen niets anders, wanneer we tafeltjes leren. Als de oplossing van de opgave een formule is, zijn er geen standaard antwoorden uit je hoofd te leren. Dan wordt je gedwongen de juiste methode te gebruiken, en elke stap naar de oplossing correct uit te voeren.
Ten vierde zorgt deze methode ervoor dat de leerling gaat herkennen hoe de verschillende oplossingsmethoden met elkaar samenhangen, ontdekt dat de opgaven in dezelfde paragraaf steeds met dezelfde methode opgelost kunnen worden, in plaats van te menen dat elke opgave een uitzondering is en op een andere manier opgelost moet worden.
Ten vijfde maakt dit enkele onderdelen van de wiskunde makkelijker, zoals het opstellen van formules voor lineaire en hogeremachtsfuncties, evenals later het schrijven van computeralgoritmes.
Ten zesde, en waarschijnlijk ten belangrijkste, leert de leerling om algoritmen te creëren voor wiskundige bewerkingen buiten de wiskunde, in de andere exacte vakken.
Stel ik dan voor om leerlingen niet meer te leren rekenen?
Natuurlijk niet. Leerlingen moeten leren rekenen.
Rekenen is een kunde die je elke dag nodig hebt.Maar wiskundeleerlingen leren toch al niet rekenen. Zij moeten al kunnen rekenen voordat ze wiskunde kunnen leren.
Rekenen leer je op de basisschool.
Op de middelbare school leer je af hoe je moet rekenen.Je leert aan, hoe je formules op een rekenmachine uitwerkt.
Ik heb leerlingen die na drie jaar middelbare school de simpelste berekening met de rekenmachine moeten uitvoeren, omdat "dat sneller gaat", of ze "het anders niet weten".
Dat is triest.
Daarom naast het bovenstaande voorstel een tweede:
Geef naast wiskunde op de middelbare school ook rekenen als officieel examenvak.
Laat leerlingen weer weten hoe ze moeten hoofdrekenen, optellen, aftrekken, delen, vermenigvuldigen.Leer ze uitkomsten te schatten van wortels en machten, leer ze waar ze mogen gokken en waar niet.
Leer leerlingen hoe zij hun eigen oplossingen kunnen controleren.
Scheid wiskunde van rekenen, zodat leerlingen het verschil herkennen tussen het opstellen van algoritmen om van een opgave naar een oplossing te komen, en het bewerken van getallen.
En als laatste een oproep aan wiskundeleraren en het Ministerie van Onderwijs:
Hou op met pretenderen dat wiskunde een moeilijker vorm van rekenen is,
die je alleen kunt leren als je al kunt rekenen.Hou op met te pretenderen dat je ook kunt rekenen als je wiskunde beheerst.
Met de huidige vorm van wiskunde hoef je niet te kunnen rekenen.De rekenmachine is heel goed in staat alle berekeningen voor je uit te voeren en genereert rekenkundig gemakzucht.
Wiskunde moet zich contentreren op het creëren van algoritmen, naar de vraag "hoe los ik dit op?" in plaats van naar de vraag "wat is de oplossing?".