De stelling van Pythagoras in het meervoud - ΩJr. Wiskunde en Bijles
Deze informatie leeft op een webpagina op hetvolgende webadres: 'https://omegajunior.globat.com/wiskunde/'.
Hoensbroek, 2001-07-01
Een van mijn wiskundeleerlingen moest de lengte van een diagonale lijn uitrekenen uit een balk. Normaliter gebruik je hiervoor tweemaal de stelling van Pythagoras. Kan dat ook in 1 keer?
Jazeker. Dit artikel legt uit hoe.
Opdracht: bereken de lengte van lijn CE in onderstaande balk:
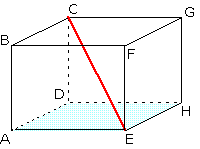
Normaliter gebruik je hiervoor 2x de stelling van Pythagoras (a² + b² = c²). Als eerste bepaal je het vlak waarin de lijn CE ligt. Dit kunnen er 2 zijn, en in dit geval heb ik gekozen voor het vlak DCFE. Zie onderstaand figuur.
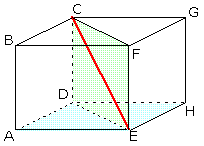
Je rekent de lengte uit van lijn CF: CF² = BC² + BF². Hierna neem je het vlak DCFE uit de balk en zet hem apart:
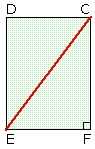
Uit dit vlak bereken je tenslotte lijn CE: CE² = EF² + CF².
Genoemde wiskundeleerling echter, nam een afkorting. Zij bedacht: als ik eerst CF uitreken, om hem daarna weer te moeten gebruiken, kan ik dan CE ook in 1 keer uitrekenen? En ze rekende: CE² = EF² + BF² + BC². Het figuur hieronder geeft de route langs de berekening weer:
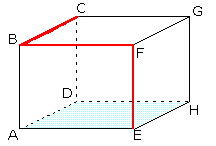
Ik kende deze methode niet, dus moest ik het narekenen, maar mijn leerling had gelijk. Hiermee heeft ze uit geheel eigen inzicht 2 stellingen van Pythagoras gecombineerd tot 1 meervoudige. Zo leer je als leraar nog iets.
De voordelen van de meervoudige stelling van Pythagoras:
Bijstelling op 15 september 2002:
Ik heb laatst een wiskundeboek van 4 vmbo ingezien. Daar stond een voorbeeld van de meervoudige stelling in vermeld. (Dat zouden ze meer moeten doen!)

Normaliter gebruik je hiervoor 2x de stelling van Pythagoras (a² + b² = c²). Als eerste bepaal je het vlak waarin de lijn CE ligt. Dit kunnen er 2 zijn, en in dit geval heb ik gekozen voor het vlak DCFE. Zie onderstaand figuur.

Je rekent de lengte uit van lijn CF: CF² = BC² + BF². Hierna neem je het vlak DCFE uit de balk en zet hem apart:

Uit dit vlak bereken je tenslotte lijn CE: CE² = EF² + CF².
Genoemde wiskundeleerling echter, nam een afkorting. Zij bedacht: als ik eerst CF uitreken, om hem daarna weer te moeten gebruiken, kan ik dan CE ook in 1 keer uitrekenen? En ze rekende: CE² = EF² + BF² + BC². Het figuur hieronder geeft de route langs de berekening weer:

Ik kende deze methode niet, dus moest ik het narekenen, maar mijn leerling had gelijk. Hiermee heeft ze uit geheel eigen inzicht 2 stellingen van Pythagoras gecombineerd tot 1 meervoudige. Zo leer je als leraar nog iets.
De voordelen van de meervoudige stelling van Pythagoras:
- Sommige leerlingen hebben moeite om te herkennen in welk ruimtelijk vlak lijn CE ligt. Deze zouden baat kunnen hebben bij het "rekenen langs de route";
- De bewerking duurt minder lang dan 2x de enkelvoudige stelling, zowel in denk- als rekenwerk;
- Er worden minder berekeningen gemaakt zodat de kans op fouten afneemt;
- Ook als de "route" ingewikkeld wordt (het werkt ook bij 3x, 4x, enz.), blijft de bewerking eenvoudig.
Bijstelling op 15 september 2002:
Ik heb laatst een wiskundeboek van 4 vmbo ingezien. Daar stond een voorbeeld van de meervoudige stelling in vermeld. (Dat zouden ze meer moeten doen!)