Vermenigvuldigen met strepen: zo werkt dat! - ΩJr. Wiskunde en Bijles

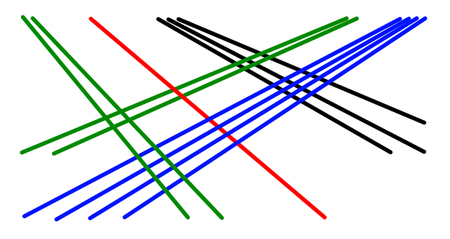
Fig. 1: visuele representatie van het getal 5112
Hoe kom je daar nou bij?

Vooraan beginnen. Dit is 2x3:

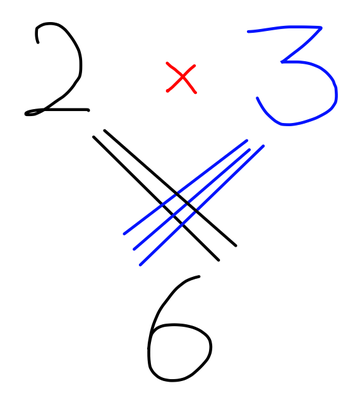
Fig. 2: de vermenigvuldiging van 2 maal 3

Vanuit het cijfer 3 lopen er 3 strepen schuin naar linksonder. Vanuit het cijfer 2 lopen er 2 strepen schuin naar rechtsonder. Ze kruisen elkaar in het midden. Tel de kruisingen op: het zijn er 6.

Moeilijker. Dit is 12x3:

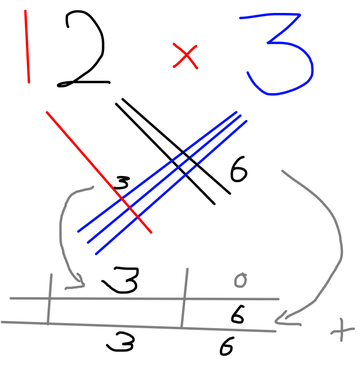
Fig. 3: 12 keer 3 = 36

Even van rechts naar links nalopen:

Vanuit het cijfer 3 lopen er weer 3 strepen schuin naar linksonder. Vanuit het cijfer 2 lopen er weer 2 strepen schuin naar rechtsonder. Die kruisen elkaar. Tel de kruisingen op: het zijn er 6.

Nieuw: vanuit het cijfer 1 loopt er een nieuwe streep schuin naar rechtsonder. Die kruist de strepen van het cijfer 3 ook! Tel deze kruisingen op: het zijn er 3. Deze tellen echter als 10x zoveel, dus als 30.

Zie hoe we kolommen kunnen tekenen om de aantallen kruising in te noteren. Dat lijkt nu overbodig, maar ik beloof dat het goed van pas komt als het moeilijker wordt.

Tel op: 6 + 30 = 36.


Variatie: Dit is 14x5:

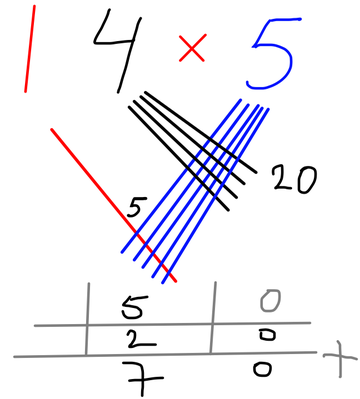
Fig. 4: 14 maal 5 = 70

Tellen als een meikever: 4 lijnen kruisen 5 lijnen 20 keer, dus 4x5=20.

Moeilijker. Dit is 12 maal 13:

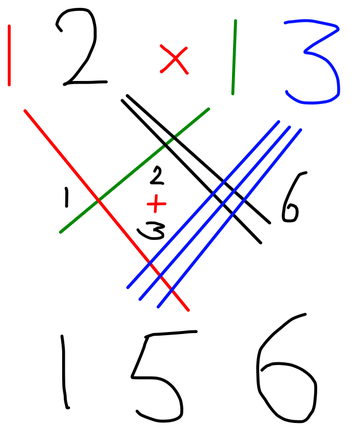
Fig. 5: 12 x 13 = 156

Even van rechts naar links nalopen:

Vanuit het cijfer 3 lopen er weer 3 strepen schuin naar linksonder. Vanuit het cijfer 2 lopen er weer 2 strepen schuin naar rechtsonder. Die kruisen elkaar. Tel de kruisingen op: het zijn er 6.

Vanuit het nieuwe, rechter cijfer 1 loopt er een nieuwe streep schuin naar linksonder. Die kruist de 2 strepen van het cijfer 2. Tel deze kruisingen op: het zijn er 2. Deze tellen als 10x zoveel, dus als 20.

Daaronder zien we vanuit het linker cijfer 1 een bekende streep schuin naar rechtsonder. Die kruist de 3 strepen van het cijfer 3. Tel deze kruisingen op: het zijn er 3. Deze tellen ook als 10x zoveel, dus als 30.

En meest links: de beide strepen die uit de beide cijfers 1 naar elkaar toelopen, die kruisen elkaar ook nog! Dat levert 1 extra kruising op, die telt als honderdtal. Dat levert dus 100 op.

Tel op: 6 + 20 + 30 + 100 = 156.

Omdat geen van de optellingen in deze opgave een tiental overschreed, was het gebruik van kolommen niet nodig.


Variatie. Probeer eens 27 keer 37:

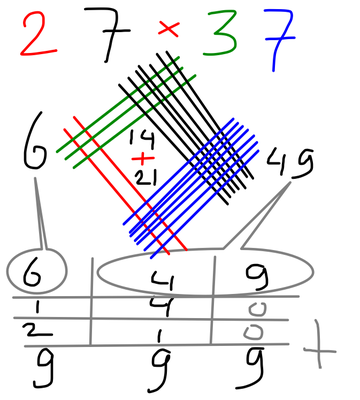
Fig. 6: 27 x 37 = 999

En dan bieden de kolommen hulp: ken de kruisingen aan de juiste kolommen toe en plaats extra nullen waar nodig.

En kan dat ook met getallen van 3 cijfers?

Jawel. Bijvoorbeeld 213 vermenigvuldigd met 24:

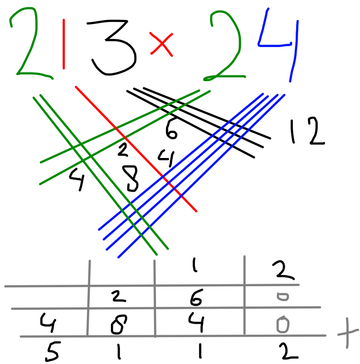
Fig. 7: 213 x 24 = 5112

Heb je gemerkt dat de 4e nieuwe kruising ook een 4e kolom opleverde? En dat die ook meteen als duizendtal gold?

Achtergrond

Ik merkte dit rekenhulpmiddel op middels een Engelstalig bericht op Google+, van mevrouw Christy Ramsey, die beweerde dat dit hulpmiddel in Japan werd gebruikt om kinderen te leren vermenigvuldigen. En inderdaad geeft het een goed inzicht in hoe een multiplicatie werkt. Zij heeft ook uitgewerkt hoe getallen van 3 en 4 cijfers uit te rekenen.

Nadeel van dat bericht was dat de kruisingen niet schuin genoeg stonden: er werd nagenoeg een vierkant getekend, met horizontale en verticale lijnen. Dan wordt het lastig om de kolommen van tientallen, honderdtallen, en duizendtallen te herkennen, en dus ook om de aantallen kruisingen op de juiste wijze op te tellen.

Dus heb ik wat geëxperimenteerd tot ik op de boven getoonde schuingetekende weergave uitkwam. Zo is het te herkennen wat een tiental, en wat een honderdtal is, en kunnen de kolommen makkelijk worden getekend, mocht dat nodig zijn.

Vanuit de reacties op het originele bericht werd duidelijk dat dit rekenhulpmiddel ook wordt aangeleerd op Amerikaanse scholen. Mijn vrouw, die van Amerikaanse afkomst is, kende hem niet. Ik ben hem zelf ook niet tegengekomen op de Nederlandse scholen.


Hebben jullie dit al eens eerder gezien?